導(dǎo)讀

本文分入門篇和進(jìn)階篇。本期是入門篇，主要闡述MPN的歷史和意義，幫你理解MPN。主要是意會(huì)。進(jìn)階篇會(huì)告知MPN的數(shù)學(xué)原理，就是MPN值是怎么算出來(lái)的。進(jìn)階篇閱讀有難度，需具備一定的數(shù)學(xué)基礎(chǔ)。

?

引子

剛?cè)肼毜男∶鞒闪艘幻鈽s的微生物試驗(yàn)員，在工作幾天后，他懷著崇敬而期待的心情問(wèn)了師父一個(gè)問(wèn)題：“啥是MPN？”

師父平靜的回答：“最大可能數(shù)”

小明想了想，怯怯的又問(wèn)：“那啥是最大可能數(shù)？”

師父故作高深的回答：“是一種用統(tǒng)計(jì)學(xué)算出來(lái)的樣品中最可能的數(shù)！”

小明又想了想，又問(wèn)：“這個(gè)數(shù)有什么意義？它是怎么算的？”

師父悠悠的回了一句：“今天的培養(yǎng)皿都洗了么？三角瓶呢？鹽水滅了沒(méi)？”

小明聽聞，驚恐而遁。

師父凝望小明背影，回身遙望窗外，心想：“20年了，我干這行20年了，當(dāng)年我也是這么問(wèn)的師父，但是沒(méi)有答案，誰(shuí)能告訴我啊，啥是MPN~~~~~~~~~~~~”

入門篇

?

要想說(shuō)清楚MPN，就首先要了解發(fā)酵管計(jì)數(shù)法（稀釋計(jì)數(shù)法）。

有些樣品是不適合用平板法計(jì)數(shù)的，比如菌含量很低的，或者有雜質(zhì)干擾的樣品。菌含量很低的樣品中最典型的是水。所以發(fā)酵管計(jì)數(shù)法主要用于水質(zhì)中大腸類細(xì)菌的檢測(cè)。有資料顯示這種方法最早出現(xiàn)在1875年前后，巴斯德用此種方法做過(guò)菌數(shù)檢測(cè)，之后李斯特等人也用過(guò)這種方法，20世紀(jì)初已經(jīng)廣泛應(yīng)用于水質(zhì)檢測(cè)。

那么發(fā)酵管法是怎么計(jì)數(shù)的呢？其實(shí)很簡(jiǎn)單，比如一個(gè)水樣，將其稀釋10倍、100倍和1000倍，每個(gè)稀釋度分別取1mL稀釋液接種1管發(fā)酵管（比如乳糖膽鹽肉湯）。如果10倍和100倍生長(zhǎng)，1000倍不生長(zhǎng)，那么可以粗略的認(rèn)為1mL水樣中的菌含量在100-1000個(gè)之間。

后來(lái)又有進(jìn)步。比如還按上面的例子，稀釋倍數(shù)不變，每個(gè)稀釋度接種管數(shù)從1管變成5管，培養(yǎng)后10倍5管全長(zhǎng)，100倍5管有4管生長(zhǎng)，1000倍都不長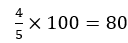(zhǎng)。那么計(jì)算方式改為。結(jié)果就變成了1mL水樣中的菌含量是80個(gè)。

是不是先進(jìn)了很多？但是以你今天的眼光看，這簡(jiǎn)直弱爆了，對(duì)么？

但是你考慮過(guò)么？當(dāng)時(shí)的中國(guó)還處于清朝。

頓時(shí)，你是不是又覺(jué)得，這簡(jiǎn)直太先進(jìn)了~~~~

這種發(fā)酵管計(jì)數(shù)的結(jié)果不準(zhǔn)，你看到了。還有一個(gè)人也看到了，他就是M. H. McCrady，就職于加拿大魁北克省衛(wèi)生委員會(huì)實(shí)驗(yàn)室。1915年一篇雄文問(wèn)世，MPN的名號(hào)從此響徹江湖。

《The Numerical Interpretation of Fermentation-Tube Results》（譯：發(fā)酵管結(jié)果的數(shù)值解釋），發(fā)表于美國(guó)《傳染病雜志》。他用概率論方法分析了發(fā)酵管計(jì)數(shù)的結(jié)果，從而第一次提出了MPN（Most Probable Number）的叫法，并算出了最早的MPN表。

之后，專業(yè)的數(shù)學(xué)家紛紛登場(chǎng)，開始將此方法進(jìn)行完善。Halvorson和Ziegler（1933），Eisenhart和Wilson（1943）和Cochran（1950）發(fā)表了有關(guān)MPN法統(tǒng)計(jì)學(xué)基礎(chǔ)的文章。 Woodward（1957）建議MPN表應(yīng)省略那些不可能的陽(yáng)性組合（如：0-0-3）。 De Man（1983）發(fā)布了置信區(qū)間方法。

至此，MPN法才變成了今天我們看到的樣子。

?

好了，背景介紹完了，現(xiàn)在開始幫助大家理解MPN的意義。這里會(huì)提到一些統(tǒng)計(jì)學(xué)的概念，但沒(méi)有計(jì)算，計(jì)算留在進(jìn)階篇。沒(méi)辦法，MPN畢竟是統(tǒng)計(jì)學(xué)基礎(chǔ)上算出來(lái)的，想一點(diǎn)統(tǒng)計(jì)學(xué)概念不提就解釋清楚太難了。

我們以大腸菌群MPN法為例。我們把1mL樣品接入一管LST，培養(yǎng)后結(jié)果只會(huì)有兩種可能，產(chǎn)氣或不產(chǎn)氣。從根源上說(shuō)就是陽(yáng)性或陰性。那么這種只有兩種結(jié)果的試驗(yàn)，在統(tǒng)計(jì)學(xué)上叫伯努利試驗(yàn)。生活中還有很多例子，比如電源只有開和關(guān)，比如拋硬幣，只有正面和反面。沒(méi)有中間的立場(chǎng)，沒(méi)有妥協(xié)的余地。

?

我們MPN法試驗(yàn)一般都是9管，3個(gè)稀釋度，每個(gè)稀釋度3管。那么相當(dāng)于把伯努利試驗(yàn)分了3組，每組做了3次。每組內(nèi)的3管之間的結(jié)果沒(méi)有相互干擾，是相互獨(dú)立的，發(fā)生的概率也是一樣的。這種每組內(nèi)的3次試驗(yàn)就叫n重伯努利試驗(yàn)。比如拋硬幣，你連續(xù)拋20次，每次只有兩種可能，正面和反面，而且第一次拋出的結(jié)果，對(duì)第二次拋出正面還是反面沒(méi)有任何影響。

至此，基本概念已經(jīng)建立起來(lái)，為了幫助理解，我們拋開微生物，開始玩拋硬幣游戲。

準(zhǔn)備一個(gè)硬幣，連續(xù)拋20次，請(qǐng)問(wèn)正面能有幾次？

理論上，0-20次，皆有可能。有人運(yùn)氣無(wú)敵，連續(xù)20次正面。有人運(yùn)氣也無(wú)敵，一個(gè)正面都沒(méi)有。到底最可能幾次正面呢？伯努利概型是有公式的，所以來(lái)看計(jì)算結(jié)果吧。

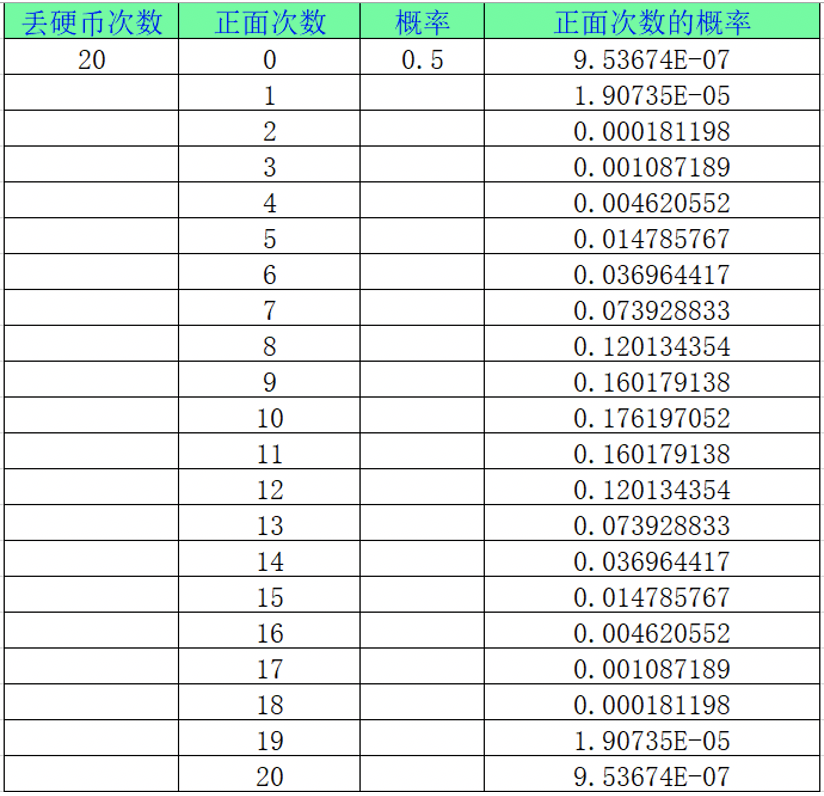
表格不好看？ 那我們換成圖。

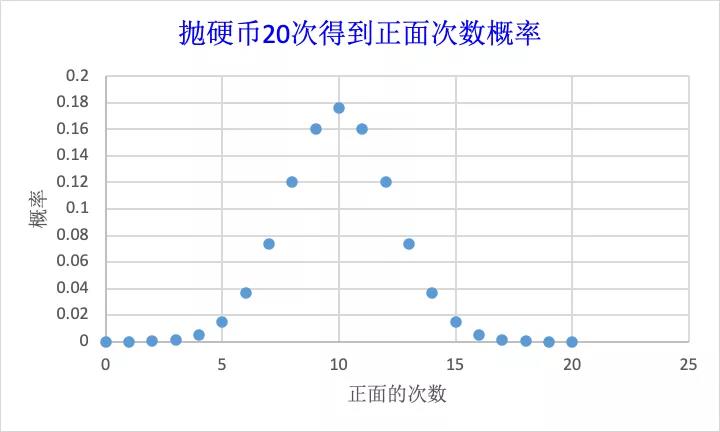
從這個(gè)圖看，是不是一目了然。這就是二項(xiàng)式分布，也叫伯努利分布。在0-20次正面的所有可能中，得到10次正面的概率最高。那么10次就是拋20次硬幣后，最可能得到的正面次數(shù)。也可以說(shuō)，是這個(gè)命題下的最大可能數(shù)。

?

明白了么？MPN值就是在現(xiàn)有因素下能推算出的微生物含量概率最大的那個(gè)濃度。

MPN法不像平板法，平板法能直觀的去數(shù)平板上的菌數(shù)，所以平板法得到的結(jié)果是真實(shí)的，是你試驗(yàn)出來(lái)的，數(shù)出來(lái)的。而MPN法的結(jié)果是通過(guò)幾根試管的陰陽(yáng)性，通過(guò)統(tǒng)計(jì)學(xué)推算出的樣品中的最可能的濃度。由于這個(gè)結(jié)果是推算的，為了與平板法的真實(shí)結(jié)果相區(qū)分，所以有了新的單位MPN。

比如試管陽(yáng)性2-1-0，通過(guò)MPN表查的結(jié)果是15，置信區(qū)間3.7-42?，F(xiàn)在單位是15MPN/g，如果改成15個(gè)菌/g，你是不是就更好理解了？

這里面的3.7-42，就類似上述拋硬幣游戲正面次數(shù)的范圍0-20，只是范圍更小，因?yàn)槭?5%置信區(qū)間。15就相當(dāng)于拋硬幣最可能的那個(gè)10。

?

還不明白？那請(qǐng)從入門篇再讀一邊。再讀還不明白？那就默默點(diǎn)左上角的叉叉?。?！

拋硬幣出現(xiàn)10次正面的概率并沒(méi)有想象中的那么高，只有17.6%，但是這已經(jīng)是最可能出現(xiàn)的數(shù)了。你會(huì)不會(huì)覺(jué)得MPN法的結(jié)果不準(zhǔn)？不用擔(dān)心。McCrady先生當(dāng)年都做過(guò)試驗(yàn)驗(yàn)證過(guò)，準(zhǔn)的。

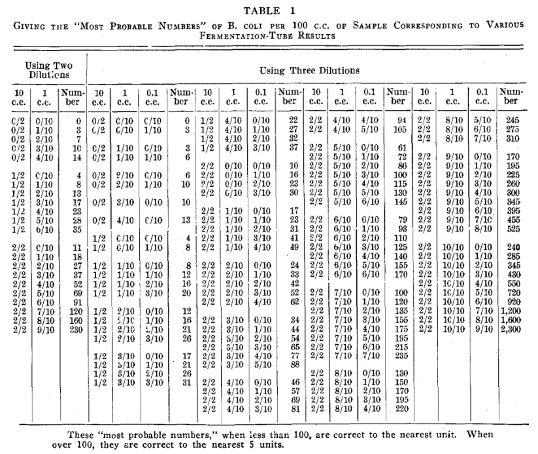
試驗(yàn)是這么做的。做大腸檢測(cè)，用同一份樣液，做了76組，每組10管。每組的10mL接種液是一次取出，再分別加入10支試管。一共做了760支，最終陽(yáng)性管數(shù)597支，然后又用陽(yáng)性率計(jì)算出了10支試管中陽(yáng)性管數(shù)的分布，發(fā)現(xiàn)和實(shí)際試驗(yàn)情況基本一致。具體看下表。

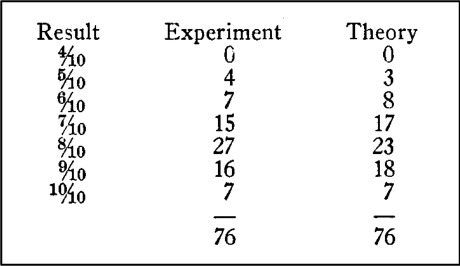
左側(cè)起，第一列是10管中陽(yáng)性的管數(shù)，比如4/10，就是一組10支有4支陽(yáng)性。第二列是當(dāng)時(shí)做試驗(yàn)的情況，第三列是通過(guò)概率計(jì)算出的情況。

例如，我們以7/10為例，就是10支試管有7支陽(yáng)性的，試驗(yàn)中76組試驗(yàn)，每組7支陽(yáng)性的組數(shù)是15組，而概率計(jì)算得出的組數(shù)是17組，所以偏差不是很大，整體試驗(yàn)情況和理論計(jì)算情況基本一致。說(shuō)明統(tǒng)計(jì)學(xué)計(jì)算在微生物領(lǐng)域是適用的，MPN法的準(zhǔn)確性是靠譜的。

拋硬幣的概率是明確的，正面的概率就是0.5，所以很好計(jì)算，圖形也很對(duì)稱。但微生物的實(shí)際情況是我們不知道陰陽(yáng)性的概率。那么在下期的進(jìn)階篇，我們就會(huì)看到如何假設(shè)一個(gè)概率，又如何通過(guò)這個(gè)假設(shè)的概率算出樣品中微生物的濃度。

?

?

參考文獻(xiàn)：

1．? McCrady, M. H. 1915. The numerical interpretation of fermentation-tube results. J. Infect. Dis. 17:183-212.

2．? U.S. Food & Drug Administration. BAM Appendix 2: Most Probable Number from Serial Dilutions.

3．? 王明慈, 沈恒范. 概率論與數(shù)理統(tǒng)計(jì). 高等教育出版社. 1999年.

未完待續(xù)